Solving 2 Linear equations

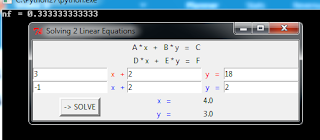
The next code is based on the Gauss Elimination method for solving a system of linear equations.

# Gauss elimination method for 2 linear equations
import Tkinter as tk

def lab_1(txt, foreground, row, col):
    w = tk.Label(root, text = txt, fg = foreground)
    w.grid(row = row, column = col)
    return w  

def lab_2(txt, row, col, cs):
    w = tk.Label(root, text = txt)
    w.grid(row = row, column = col, columnspan = cs)
    return w

def lab_3(txt):
    w = tk.Label(root, text = txt)
    return w

def ent_1(txt_var, width_e, row, col):
    w = tk.Entry(root, textvariable = txt_var, width = width_e)
    w.grid(row = row, column = col)
    return w
#tk.Button(root, text = "-> SOLVE", borderwidth = 4, command = solve_le)
def button(txt, border_width, cmd, row, col, rs, cs):
    b = border_width
    t = txt
    w = tk.Button(root, text = t, borderwidth = b,  command = cmd)
    w.grid(row = row, column = col, rowspan = rs, columnspan = cs)
    return w

def solve_le():
    if a_val.get() == 0:
        print "The value of 'a' must be greater than 0"
    else:
        a = a_val.get()
        b = b_val.get()
        c = c_val.get()
        d = d_val.get()
        e = e_val.get()
        f = f_val.get()

        nf = - d/a

        d_n = nf * a + d
        e_n = nf * b + e
        f_n = nf * c + f

        y = f_n / e_n
        x = (c - b * y) / a

        print "nf =", nf

        x_result.config(text = x)
        x_result.grid(row = 4, column = 3, sticky = tk.W, columnspan = 2)

        y_result.config(text = y)
        y_result.grid(row = 5, column = 3, sticky = tk.W, columnspan = 2)


""" Starting with Tkinter codes ... """
root = tk.Tk()

root.title("Solving 2 Linear Equations")

w_lbl = 3
w_ent = 19

b_txt = "-> SOLVE"
b_brw = 4
b_row = 4
b_col = 0
span1 = 2
span2 = 5

RED  = "red"
BLUE = "blue"

a_val, b_val, c_val = tk.DoubleVar(), tk.DoubleVar(), tk.DoubleVar()
d_val, e_val, f_val = tk.DoubleVar(), tk.DoubleVar(), tk.DoubleVar()

eq_1_str = " A * x   +   B * y   =   C"
eq_2_str = " D * x   +   E * y   =   F"

lab_2(eq_1_str, 0, 0, span2)
lab_2(eq_2_str, 1, 0, span2)


"""  <<<<  Entries  >>>>  """
ent_1(a_val, w_ent, 2, 0)
ent_1(b_val, w_ent, 2, 2)
ent_1(c_val, w_ent, 2, 4)
ent_1(d_val, w_ent, 3, 0)
ent_1(e_val, w_ent, 3, 2)
ent_1(f_val, w_ent, 3, 4)

"""  <<<<  Labels   >>>>  """
lab_1(" x   +" ,  RED, 2, 1)
lab_1(" y   = ",  RED, 2, 3)
lab_1(" x   +" , BLUE, 3, 1)
lab_1(" y   = ", BLUE, 3, 3)
lab_1(" x   = ", BLUE, 4, 2)
lab_1(" y   = ", BLUE, 5, 2)
x_result = lab_3(" ")
y_result = lab_3(" ")

"""  <<<<  Button   >>>>  """
button(b_txt, b_brw, solve_le, b_row, b_col, span1, span1)

root.mainloop()
 

The results are going to be approximations because of the nature of the code, naturally.

Testing with the next pair of equations:

  3  * x1 + 2 * x2 = 18
(-1) * x1 + 2 * x2 = 2